Welcome
NumberDB is a collaborative database of numbers. The underlying idea is that in practise, numbers are determined by their first 10 digits. That makes them searchable. NumberDB attempts to be a tool to identify numbers, and to show known descriptions. Which numbers are stored depends on their simplicity and their relevance. NumberDB stores numbers in tables. Tables are families of numbers together with a description. Thus a number can appear in several tables: For example, the number 1 is in the table of Integers, Values of the Gamma function, and it has its own table One as it is a special number. Tables of numbers also contain a definition, a description of parameters, and possibly formulas, comments, references, links, programs, and further more specific information. Furthermore tables are given tags, which helps searchability and classification.How to search
The searchbar can be used to search for:-
Real numbers:Enter the number in one of three formats:
- Decimal representation including the period, e.g. "3.14" to search for pi. The search will be done in an interval around the entered number: Entering "3.14" will search for numbers in the interval (3.13, 3.15).
- Scientific notation (no period necessary), e.g. "14e2" to search numbers between 1300 and 1500.
- NumberDB's p-notation: Enter a term of the form "ApB", where A and B are integers. It corresponds to the number 10A · 0.B, e.g. "1p314" for pi. The sign of the number is determined by the sign of B.
-
Fractional parts of real numbers:Enter the first few digits after the period, e.g. "1415" for pi.
-
Integers:Enter the exact integer without period, e.g. "-1". This works for integers with up to 127 binary digits (roughly 38 decimal digits). For longer integers, try to search them as real numbers.
-
Complex numbers:Enter sums or differences of the form "A" or "i*A" or "A*i", where "A" is a real number in the above format or a rational number. Entering "-1/2 + i * 0.86602" (to search for a third root of unity) will search within a larger square around it. Both, real and imaginary parts need sufficient precision.
-
$p$-adic numbers:Search for numbers in $\mathbb{Q}_p$ in one of two formats:
- Enter "Q2:1010" to search for $2^0 + 2^2 + O(2^5)$. Enter "Q2:1.1010" to search for $2^{-1} + 2^0 + 2^2 + O(2^5)$. For $p>10$, any $p$-adic digit needs to be given in base 10 with the same number of base 10 letters as $p$, e.g. "Q13:0102" will search for $13$-adic numbers of the form $1+2\cdot 13 + O(13^2)$. Minus signs are also interpreted, e.g. "Q3:-220" searches for $-(2 + 2\cdot 3^1) + O(3^3)$.
- Enter "3 + O(2^5)" or "2^0+2^1+O(2^5)" for numbers of the form $2^0 + 2^2 + O(2^5)$. This format also works for $\mathbb{Q}_p$, e.g. enter "3/5 + O(5^1)".
-
Polynomials over $\mathbb{Q}$:Enter polynomials over $\mathbb{Q}$ in arbitrary variables, e.g. enter "x^6+y^6-x^5*y^5+4*x*y" to search for $x^6+y^6-x^5y^5+4xy$.
-
Tables:Enter words from the table's title, keywords, tags, definition, or comments.
-
Tags:Enter the first letters of one word of a tag, e.g. "irr" for the tag "Irrational".
Advanced search guide
The advanced searchbar can be used to search for:-
Lists of real numbersUse Sage syntax to enter a number, a list of numbers, or a dictionary of the form {param: number}. The lists and dictionaries may be nested. The numbers might be given via formulas involving standard functions such as sin and sqrt, as well as standard constants such as e and pi.
Examples:-
-2, pi, esearches for certain constants. -
{n: 2^n for n in [1..10]}searches for $2^1$, ..., $2^{10}$. -
RIF(10,11)searches for all numbers contained in the interval $[10,11]$. -
{a: {b: a/b for b in [1..5] if gcd(a,b) == 1} for a in [-5..5]}searches certain small rational numbers.
-
-
Lists of complex numbersSimilarly one can search for complex numbers. Recommended parents are CIF (complex interval field), CBF (complex ball field), and SR (symbolic ring), although CC (complex field via floats) should work as well unless too much precision is lost during the computation.
-
Lists of p-adic numbersSimilarly one can search for p-adic numbers in $\mathbb{Z}_p$ and $\mathbb{Q}_p$.
Examples:-
Qp(2,prec=4)(5)searches for $5 + O(2^4)$ = $2^0 + 2^2 + O(2^4)$, that is, any $2$-adic integer with first four $2$-adic digits $1$, $0$, $1$, $0$. -
{n: Qp(2)(n) for n in [1..10]}searches $1$, ..., $10$ up to $O(2^{20})$ as $2$-adic numbers; note that 20 is the standard precision for Qp in sage.
-
-
Lists of polynomials over $\mathbb{Q}$Similarly one can search for multivariate polynomials over $\mathbb{Q}$. As only expressions are accepted (mainly for safety reasons), we can define the variables as in the following example:
-
[{n: x^2 + n for n in [1..10]} for x,y in [polygens(QQ,2,'x')]]searches for polynomials $x^2+n$ for integers $n=1,\ldots,10$, where we allow two variables $x$ and $y$.
-
Number types and displayed accuracy
Numbers in NumberDB can be of the following types.-
Integers:Integers are represented exactly as decimal numbers, e.g. "3" and "-1729".
-
Rational numbers:Rational numbers are represented exactly as fractions of integers, e.g. "-3/2".
-
Real numbers:Real numbers are usually hard to represent exactly. Instead we store an exactly represented interval that contains the real number. The smaller the interval, the higher the accuracy. The interval can be given in one of the following formats:
- Decimal expansion: e.g. "3.14" represents the interval $[3.13, 3.15]$, that is, the last digit may be off by at most $1$. Scientific notation is allowed, e.g. "12e2" represents the interval $[1100, 1300]$. Note: If the decimal expansion does not contain "." or "e", it will instead denote an exactly represented integer.
- Real interval: e.g. "[2, 2.3728596]". The end-points are exactly given.
- Real balls: e.g. "3.14 +/- 2e-2" represents the interval $[3.12, 3.16]$. The center and radius of the real ball are exactly given.
- NumberDB's p-notation: e.g. "1p31415" represents the interval [3.1414, 3.1416]. In general, for two integers A and B, "ApB" corresponds to the decimal expansion 0.BeA, where again the last digit of B may be off by 1. The sign of the number is determined by the sign of B.
-
$p$-adic numbers:$p$-adic numbers in $\mathbb{Q}_p$ are usually hard to represent exactly. Instead we store an exactly represented $p$-adic ball that contains the $p$-adic number. The smaller the radius of the ball, the higher the accuracy. The ball can be given in one of the following (equivalent) formats:
- Rational representative: e.g. "3+1/2 + O(2^3)" represents the $2$-adic ball $2^{-1} + 2^0 + 2^1 + O(2^3)$. The rational representative might be given as an algebraic expression involving integers and the usual operations "+", "-", "*", "/", and "^".
- $p$-adic expansion: e.g. "Q2:1.110" represents the $2$-adic ball $2^{-1} + 2^0 + 2^1 + O(2^3)$. Note: The most significant digit stands on the left. The $p$-adic digits are given as base 10 numbers with as many letters as the base 10 representation of p. E.g. "Q13:01.02" represents the $13$-adic ball $13^{-1}+2\cdot 13^0 + O(13^1)$. The decimal point is not necessary, e.g. "Q2:110" represents the $2$-adic ball $2^0 + 2^1 + O(2^3)$. Minus signs are allowed, e.g. "Q2:-110" represents the $2$-adic ball $-(2^0 + 2^1) + O(2^3)$.
Sage interface
Users of SageMath can perform an advanced search from within sage as in the following example.
sage: load('https://github.com/numberdb/numberdb-website/raw/main/clients/sage/numberdb-sage-interface.py')
sage: search('{n: pi^n for n in [1..5]}')
How to contribute
Contributions are possible in a number of ways:-
Bug reports, feature requests, general discussions:Visit the GitHub issue page (preferred), or send an email to info@numberdb.org.
-
Typos in tables, adding references, comments, etc.:You may edit the table's yaml file via the Guide to editing tables below. In short: Edit the corresponding yaml-file in the numberdb-data repository. The link can be found below the title on the table's webpage.
-
Contribute new tables:You may contribute new tables via the Guide to creating new tables below. In short: You need to create a table.yaml in a new folder of the numberdb-data repository and submit a pull request.
-
Programming the webpage:The webpage is in active development. Current development goals are listed in the issues section of the GitHub repository numberdb-website.
Guide to editing tables
To edit tables, you will need a GitHub account. For more advanced changes, we recommend to review the Format for tables's source code.-
Preview for editing tables
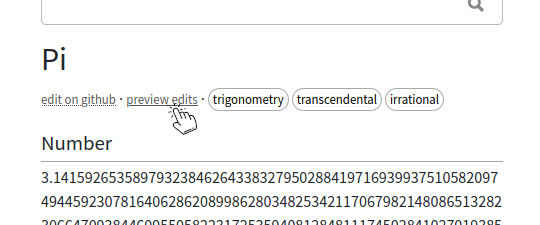
In case you want to preview your edits (or simply test what's possible), go to the table's webpage and click on "preview edits":
Make arbitrary modifications and click on "Show preview" to see how the changes will look like:
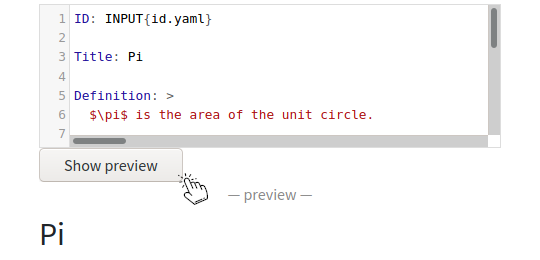
Once you are happy with the changes, copy the yaml code to the clipboard.
-
Edit table on GitHub
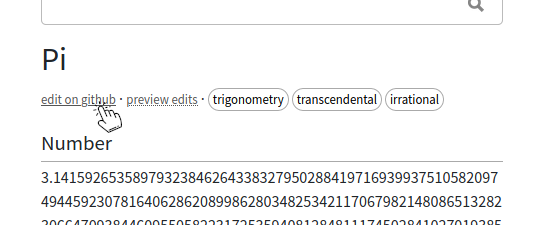
At the table's webpage click on "edit on github":
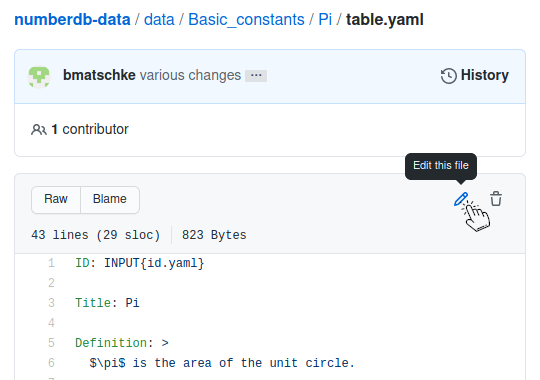
If you want to change table.yaml, click on "Edit this file":
Paste the yaml code from step 1 into the editor.
-
Save (commit) changes on GitHub
To save changes, scroll down, give your changes a title (such as "fixed typo"), give a more detailed description of the changes (if necessary), and click on commit:
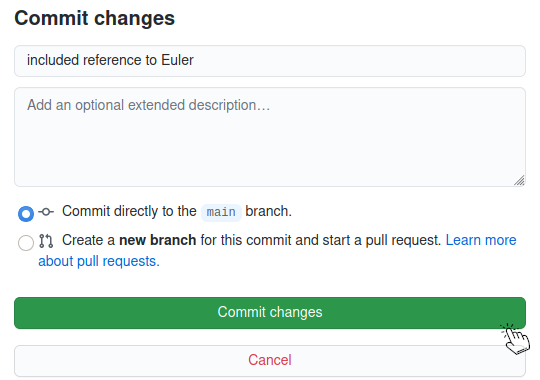
An editor will review your changes. Thanks!
Guide to creating new tables
To create new tables, you will need a GitHub account. We recommend to review the Format for tables's source code.-
Preview for new tables
We recommend that you start from the yaml code of an existing table of your choice and adjust accordingly. For this, follow the Preview step in the Guide to editing tables.
-
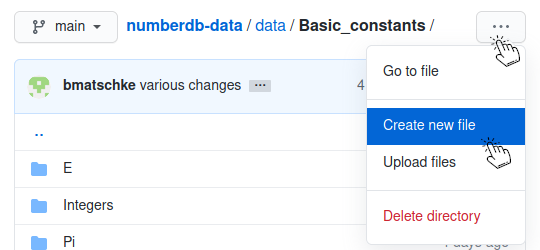
Create new table.yaml on GitHub
In the data folder of the NumberDB data repository, find a suitable folder for your table folder. As an example, we will create the "Golden ratio" table in the folder "data/Basic_constants". Go to that folder and click on "... -> Create new file":
As a filename, enter "Golden_ratio/table.yaml". (Each table has its own folder, which contains a main file "table.yaml". The folder name will work as a url for the table and should be unique without spaces.) Copy and paste the yaml code from the Preview step into the editor:
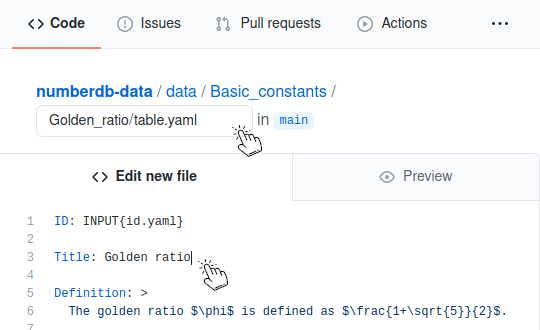
-
Save (commit) new table on GitHub
To save the new table, scroll down, give your commit a short title (such as "added golden ratio table"), give a more detailed description of the table (why it should be included, if necessary), and click on commit:
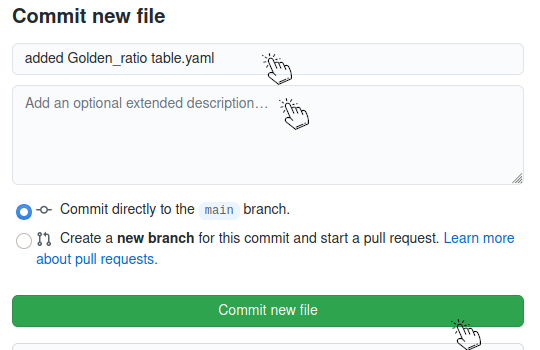
An editor will review your new table. Thanks!
Format of tables's source code
The source code of each table is written in YAML, a human-friendly language for data.
More help will come later.
Data pipeline
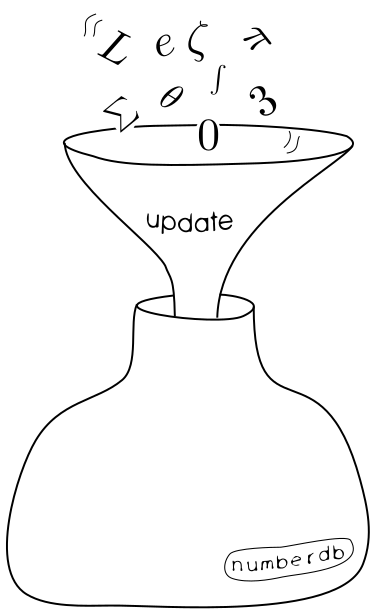
-
Raw data:The raw data is entered in human readable form (yaml) in the git repository numberdb-data on GitHub. To every new table, a bot associates an ID that serves as a permanent identifier.
-
Database builder:The raw data gets transformed regularly into the numberdb.org database. During this process, a search index is created.
-
Webpage:That database can be accessed through numberdb.org's searchbar.
Frequently asked questions
-
Why do I need to specify the period in the real number search?Because the period is even more significant than the highest digit. In principle, one could implement a search of real numbers by their first few digits without the knowledge of the period; however this would ask for numbers up to powers of 10, which does not seem natural enough in general. We implemented a search by the fractional part, as it does not depend on the base.
List of contributors
| Contributor | Number of table edits |
|---|---|
| Benjamin Matschke | 1 |

